平成１５年不動産鑑定士試験第１次試験


数　学 （問題） ｛満　点　　　１００点　　　　　時　間　　　２時間（１２：３０〜１４：３０）｝

〔注意事項〕

　　１　問題用紙及び解答用紙は、係官の指示があるまで開けてはいけません。

　　２　これは問題用紙です。解答は解答用紙に書いてください。

　　３　問題用紙は表紙を含めて３ページ、解答用紙は表紙を含めて３ページです。

　　４　解答は、解答用紙の所定の欄に、黒の鉛筆で丁寧に書いてください。ボールペン等で書くと無効となります。

　　５　答案作成のためのメモ等は、問題用紙又は解答用紙の裏面を使用してください。

　　６　問題用紙は持ち帰っても構いません。









問題　１　（４０点）　次の各問に答えなさい。解答は結果だけでなく途中の計算も示しなさい。

　（１）　式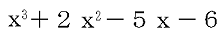　を因数分解しなさい。

　（２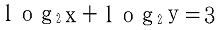）　のとき、ｘ＋ｙの最小値を求めなさい。

　（３）　地上から、初速度２９．４ｍ／秒で打上げた物体のｔ秒後の高さをｈｍとすると、ｈ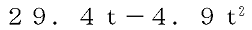＝　である。この物体

　　　　が最高点に達するまでの時間を求めなさい。

　（４）　座標平面上に点Ａ（０，−１），Ｂ（７，２），Ｃ（−１，４）とＢＣの中点Ｐがある。ベクトル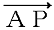上にある長さ１のベクトル

　　　　で、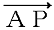と同じ向きのものを成分で表しなさい。


問題　２　（２０点）　自然数ｎに対して、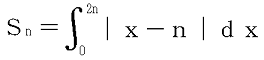とする。次の各問に答えなさい。

　（１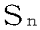）　を求めなさい。

　（２）　整式ｆ（ｘ）は、全ての自然数ｎに対して、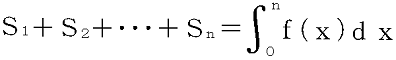を満たしている。ｆ（ｘ）を求めなさい。


問題　３　（２０点）　座標平面上に、原点Ｏ（０，０）を中心とする半径１の円Ｃがある。点Ｐ（０，２）から円Ｃに引いた２つの接線を

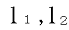　　　　とし、その接点をそれぞれＱ，Ｒとする。次の各問に答えなさい。

　（１）　点Ｑと点Ｒの座標を求めなさい。

　（２）　２つの接線　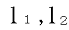と円Ｃの上半分の円周で囲まれる図形の面積を求めなさい。















問題　４　（２０点）　下図のように一辺の長さが１である立方体がある。次の各問に答えなさい。





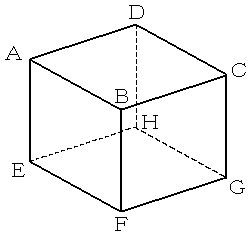
　（１）　四面体ＢＡＦＣの体積を求めなさい。

　（２）　△ＡＦＣの面積を求めなさい。

　（３）　線分ＢＨと面ＡＦＣとの交点をＰとする。線分ＢＰの長さを求めなさい。




“死格”トップページへ戻る 過去問リストへ戻る 不動産鑑定士試験に戻る